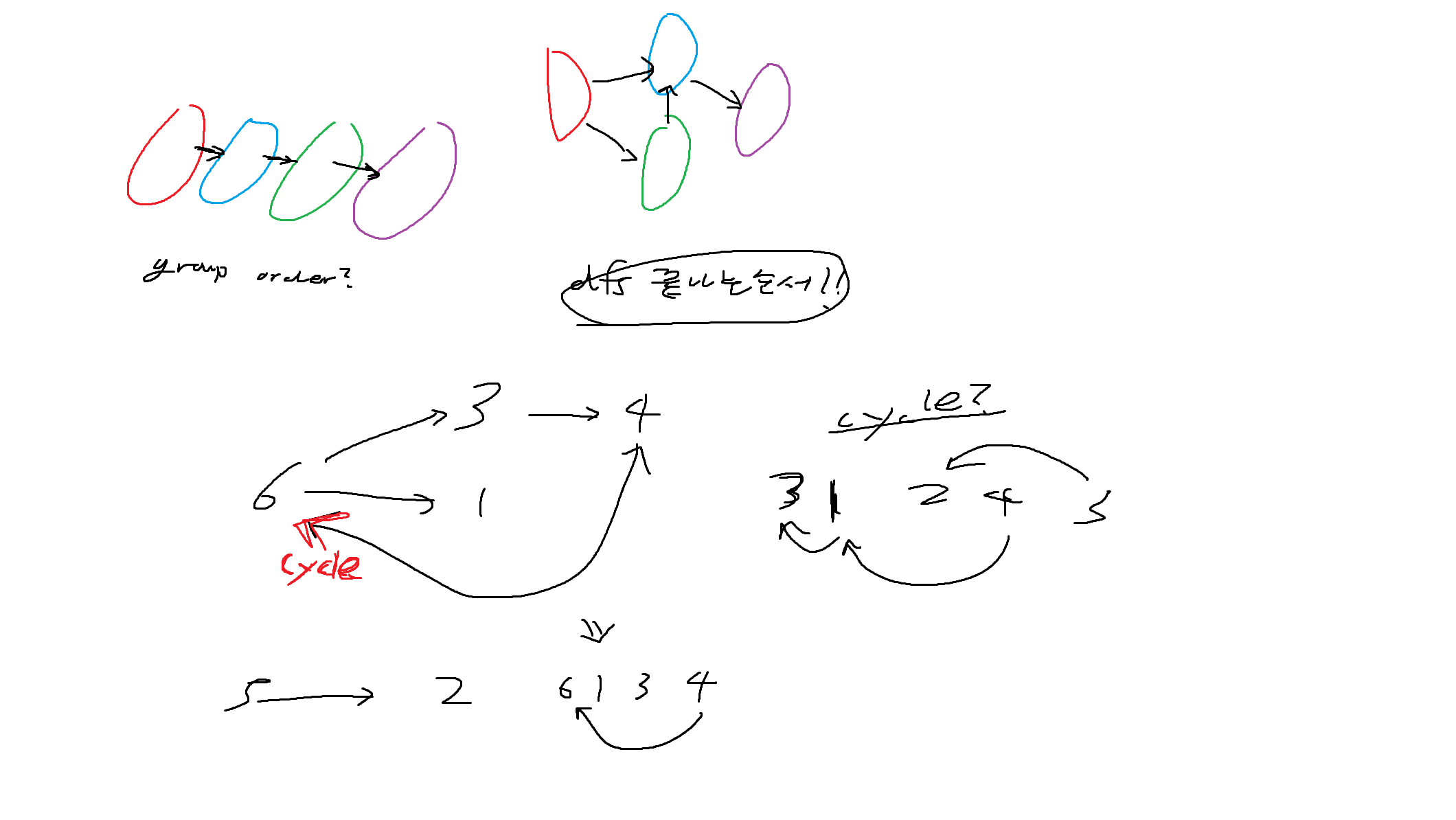(H - 1203. Sort Items by Groups Respecting Dependencies) Two-level 위상정렬

2가지 기준을 만족해야 함.

1. beforeItems가 나타내는, item간 선후관계

2. 같은 그룹 내 원소들은 항상 인접하게

 

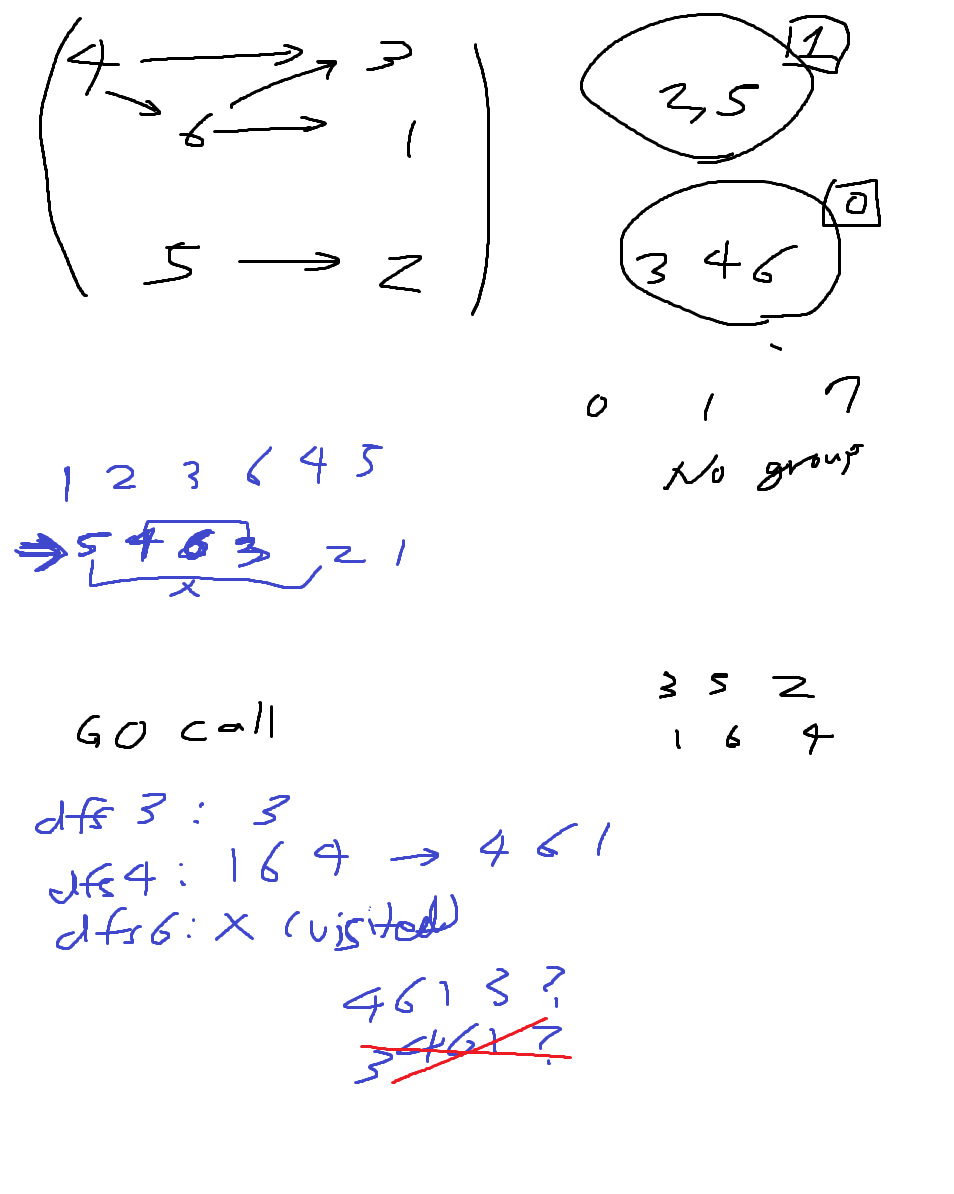
1은 topology sort 사용하면 되는게 바로 보이는데, 1을 만족하면서 동시에 2를 만족하려면?

→ 2가 만족하려면, 그룹별로도 1을 만족하도록 위상정렬이 되야함.

1에 따라 그룹 간 dependency 구한다음 위상정렬; 그 후 각 그룹 내 원소간 dependency에 따라 그룹별로 다시 위상정렬 (Two-level topology sort)

 

아이디어가 익숙하지 않아서 생각하지 못함.

설령 떠올린다 하더라도, 구현하는데 막막함.

 

https://leetcode.com/problems/sort-items-by-groups-respecting-dependencies/discuss/387977/Python-Use-DFS-to-%22detect-cycle%22-(like-210.-Course-Schedule-II-and-269.-Alien-Dictionary)

이 코드를 참고해서 C++로 구현했음.

 

---

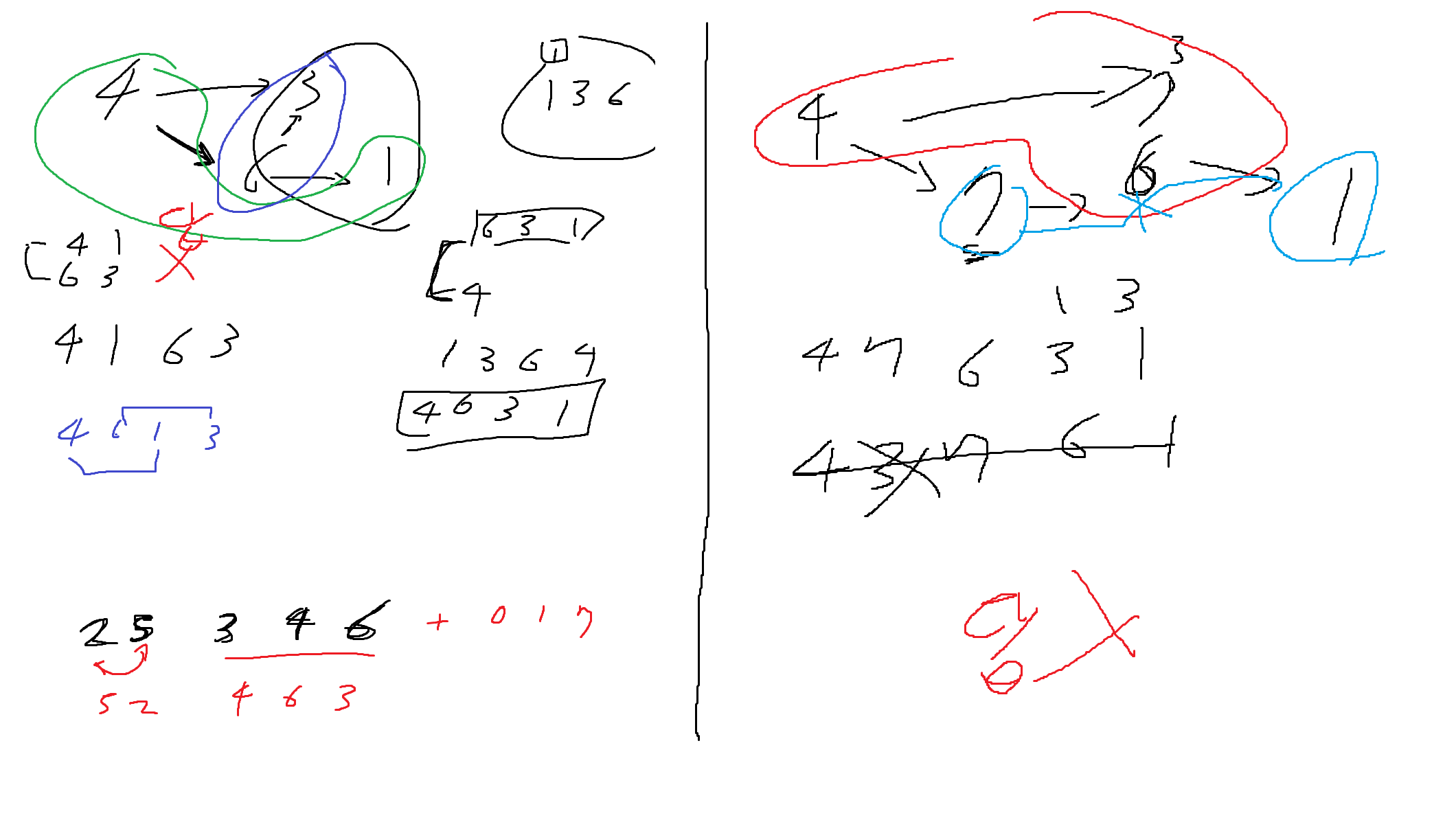
1] 가장 먼저 dependency를 표현할 자료구조

map<int, map<int,vi>> graph_items; // key : group | value : dependency within the same group (key : node | val : dependency vector)
map<int, set<int>> graph_group; // graph between groups

graph_group[1] { 2, 3, 4 } 라고 하면, 그룹 1 -> 2, 3, 4 라는 관계가 있다는 뜻.

 

graph_items는 그룹 G : 그룹 G내 원소들간의 dependency graph 를 담고있는 map

만약 Groupt 1에 2, 3, 4, 5 라는 원소가 있고, 2 -> 3, 4, 5 / 3 -> 5 라는 관계가 있다면 다음과 같이 표현됨

graph_items[1] = {2 : {3, 4, 5}, 3 : {5} } 

 

Q. 왜 map을 이용해서 이렇게 복잡하게 짰나? vector 쓰면?

-> 각 그룹에 어떤 node가 들어갈 지 모르니까, vector 쓰면 size N allocation 해야함. 비효율적이라고 생각.

 

2] topology_sort와 dfs

group graph나 item graph 중 뭐가 와도 작동할 수 있도록 template 이용해서 짬(이렇게 통일하려고 graph_group도 map을 씀)

 

★ 특히 DFS에서 cycle detection - 3-color 방법 씀

https://www.geeksforgeeks.org/detect-cycle-direct-graph-using-colors/

Detect Cycle in a directed graph using colors - GeeksforGeeks

Gray - visited, 아직 dfs안끝남 

만약 현재 노드에서 gray 노드로 이어지는 간선이 있다면? = back edge = cycle

// Visit each node using DFS + return true if there exists back edge (cycle detection)
template <class T>
bool dfs(int node, map<int, T>& graph, vi& order) {
    visited[node] = GRAY;
    for (int nxt : graph[node]) {
        if (visited[nxt] == GRAY)
            return true;

        if (visited[nxt] == WHITE && dfs(nxt, graph, order))
            return true;
    }
    visited[node] = BLACK;
    order.push_back(node);
    return false;
}

// Used in both step 2 (graph sort) and step 3 (items sort)
// T : vector<int> or set<int>
template <class T>
vi topology_sort(map<int, T>& graph) {
    vi order;

    // DFS on each graph element
    for(auto it = graph.begin(); it != graph.end(); it++){
        if (!visited[it->first])
            if (dfs(it->first, graph, order)) {
                cycleDetected = true;
                return vi();
            }
    }
    reverse(all(order));
    return order;
}

 

이렇게 짜두니까 나머지 위상 정렬은 코드 매우 간단해짐

Step 2 - group 위상정렬

Step 3 - 각 group별 items graph 넣어줘서 위상정렬 (총 그룹 개수 m번 반복)

 

 

공부한 점 : 그래프를 표현하는 복잡한 자료구조, cycle detection, 코드 모듈화 (재활용), 위상 정렬